정리) 소프트맥스 함수는 시그모이드 함수를 정규화 시킨 함수로 다중 분류에서 확률적 해석이 가능하다.
기술적으로 미분 가능하다면 어떤 함수라도 다층 신경망의 활성화 함수를 사용 가능하다.
아달린 함수(선형 활성화 함수)도 사용 가능하지만, 은닉층이나 출력층에 선형 활성화 함수를 사용하는 것이 유용하지는 않다.
복잡한 문제를 해결하기 위해서는 인공 신경망에 비선형이 필요하다.
시그모이드 함수(Sigmoid)
시그모이드 함수는 S자형 곡선 또는 시그모이드 곡선을 갖는 수학 함수를 말한다. 로지스틱 회귀는 시그모이드 함수 중 대표적인 함수이다.
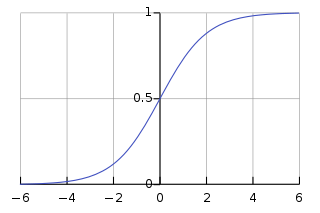로지스틱 함수
로지스틱 활성화 함수가 뉴런 개념을 가장 비슷하게 흉내 낸 함수이다.
함수 출력을 뉴런의 활성화 여부에 대한 확률로 볼 수 있다.(0-1)
하지만 로지스틱 활성화 함수는 큰 음수 입력에 대하여 문제 된다.
시그모이드 함수의 출력이 0에 가까워지게 된다.(신경망을 매우 느리게 학습)
훈련 과정에서 지역 최솟값에 갇힐 가능성이 높다.
따라서 은닉층에서 하이퍼 볼릭탄젠트가 더 선호된다.
import numpy as np
X=np.array([1, 1.4, 2.5])
w=np.array([0.4, 0.3, 0.5])
def net_input(X, w):
return np.dot(X, w)
def logistic(z):
return 1.0/(1.0+np.exp(-z))
def logistic_activation(X, w):
z=net_input(X, w)
return logistic(z)
print('P(y=1|x)=%.3f' %logistic_activation(X, w))
P(y=1|x)=0.888
위를 샘플 x가 양성 클래스에 속할 확률이 88.8%라고 해석할 수 있다.
W=np.array([[1.1, 1.2, 0.8, 0.4], [0.2, 0.4, 1.0, 0.2], [0.6, 1.5, 1.2, 0.7]])
A=np.array([[1, 0.1, 0.4, 0.6]])
Z=np.dot(W, A[0])
y_probas=logistic(Z)
print('최종 입력: \n', Z)
print('유닛 출력: \n', y_probas)
최종 입력:
[1.78 0.76 1.65]
유닛 출력:
[0.85569687 0.68135373 0.83889105]
y_class=np.argmax(Z, axis=0)
print('예측 클래스 레이블: %d' %y_class)
>>> print('예측 클래스 레이블: %d' %y_class)
예측 클래스 레이블: 0
로지스틱 회귀 & 소프트맥스 회귀
로지스틱 회귀는 2개의 선택지 중에서 1개를 고르는 이진 분류(Binary Classification)을 풀 때 사용하였지만,
로지스틱 회귀의 출력값을 확률로 해석하기 어렵다(확률 3개의 합이 1이 아니다.-확률로 해석 불가능)
떄문에 3개 이상의 선택지에서 하나를 고르는 다중 클래스 분류(Multi-class Classification)
모든 가능한 정답지에 대해서 정답일 확률의 합이 1이 되도록 하기 위해서 소프트 맥스 함수를 사용한다.
소프트맥스 함수
argmax 함수를 이용하여 최대값을 클래스 레이블로 선택할 수 있다.
softmax는 간접적인 argmax 함수로 하나의 클래스 인덱스를 반환하는 대신,
각 클래스의 확률을 반환한다.
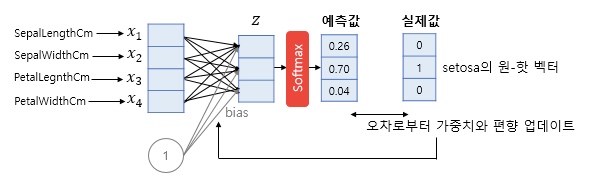
다중 클래스 환경(다중 로지스틱 회귀(multinomial logistic regression))에서 의미있는 클래스 확률을 계산할 수 있다.
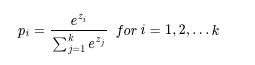
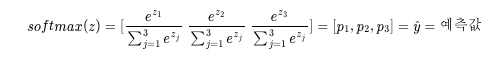
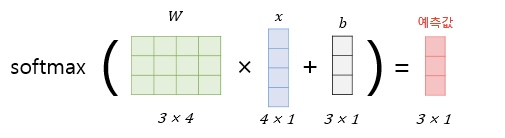
def softmax(z):
return np.exp(z)/np.sum(np.exp(z))
y_probas=softmax(Z)
np.sum(y_probas)
print('확률:\n', y_probas)
1.0
확률:
[0.44668973 0.16107406 0.39223621]
소프트맥스를 통해서 선택한 클래스 레이블은 로지스틱 출력에 argmax(최대값)을 적용한 것과 같다.
소프트 맥스는 다중 클래스일 때 의미 있는 클래스 소속 확률을 만들기 위한 정규화된 출력으로 생각할 수 있다.
텐서플로의 softmax 활성화 함수
import tensorflow as tf
Z_tensor=tf.expand_dims(Z, axis=0)
tf.keras.activations.softmax(Z_tensor)
<tf.Tensor: shape=(1, 3), dtype=float64, numpy=array([[0.44668973, 0.16107406, 0.39223621]])>
소프트맥스 함수를 사용한 다중 분류 문제의 경사 하강법 공식
다중 클래스 분류 문제에서는 크로스 엔트로피(cross entropy) 함수를 비용함수로 사용한다.
(로지스틱 비용 함수는 크로스 엔트로피 함수의 이진 분류 버전이다.)
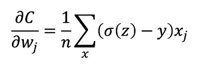
자세한 경사 하강법 공식 유도 참조
머신러닝교과서with파이썬,사이킷런,텐서플로_개정3판pg.564